mirror of
https://github.com/billbuchanan/appliedcrypto.git
synced 2026-02-21 11:18:02 +00:00
539 lines
14 KiB
Markdown
539 lines
14 KiB
Markdown

|
|
|
|
# Unit 9: Future Crypto Lab
|
|
|
|
Aim: To provide a foundation in some of the up-and-coming methods in cryptography.
|
|
|
|
**New feature:** Repl.it code additions.
|
|
|
|
## A Running a local blockchain
|
|
In a previous lab we ran our blockchain on the Ropsten test network. In this tutorial, we will run a local blockchain using ganache. We can install from:
|
|
|
|
```Solidity
|
|
https://trufflesuite.com/ganache/
|
|
```
|
|
|
|
Then download the correct version for your computer:
|
|
|
|

|
|
|
|
This should download the application file into your Downloads folder. Next go to the terminal and enter:
|
|
|
|
```
|
|
cd
|
|
cd Downloads
|
|
chmod a+x ganache-2.5.4-linux-x86_64.AppImage
|
|
```
|
|
Then run the program:
|
|
|
|
```
|
|
./ganache-2.5.4-linux-x86_64.AppImage
|
|
```
|
|

|
|
|
|
This should run the blockchain, and now select Quick start:
|
|
|
|

|
|
|
|
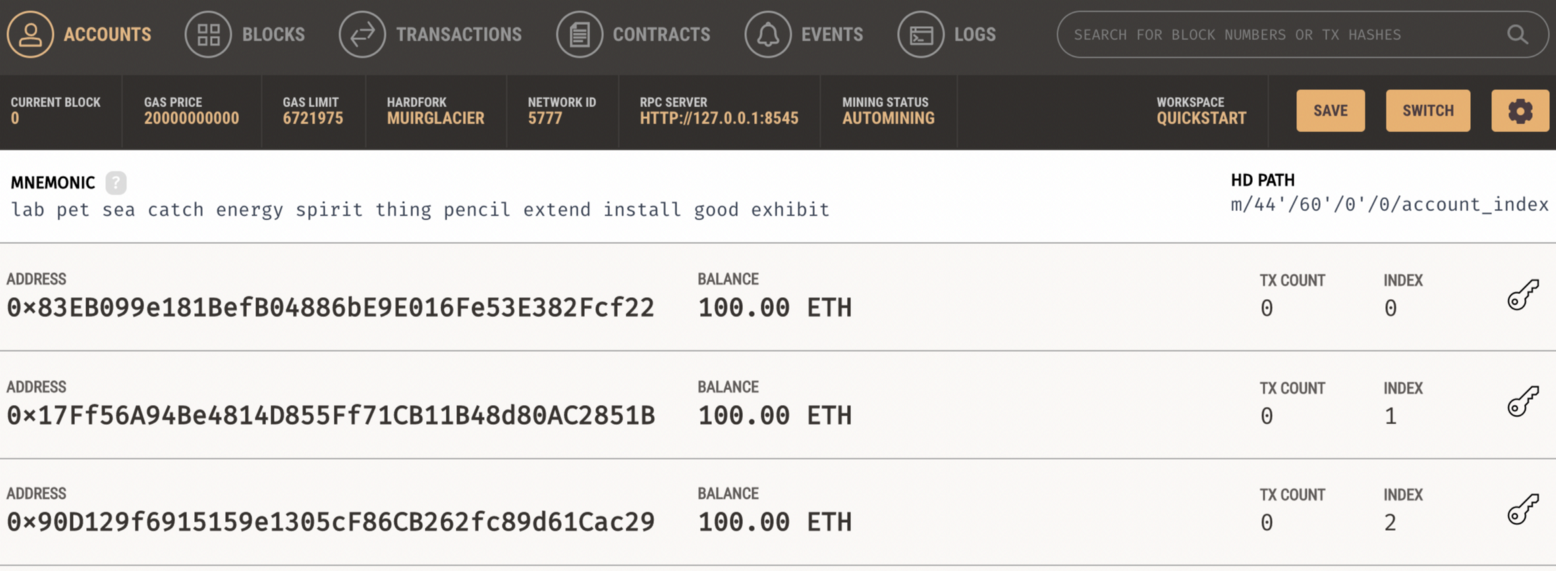
We should now have a blockchain with accounts:
|
|
|
|

|
|
|
|
## B Testing
|
|
|
|
Now with remix.ethereum.org [here](https://remix.ethereum.org), enter the following code:
|
|
|
|
```Solidity
|
|
pragma solidity ^0.8.0;
|
|
|
|
contract mymath {
|
|
|
|
function sqrt(uint x) public view returns (uint y) {
|
|
uint z = (x + 1) / 2;
|
|
y = x;
|
|
while (z < y) {
|
|
y = z;
|
|
z = (x / z + z) / 2;
|
|
}
|
|
}
|
|
function sqr(uint a) public view returns (uint) {
|
|
uint c = a * a;
|
|
return c;
|
|
}
|
|
|
|
function mul(uint a, uint b) public view returns (uint) {
|
|
uint c = a * b;
|
|
return c;
|
|
}
|
|
|
|
function sub(uint a, uint b) public view returns (uint) {
|
|
return a - b;
|
|
}
|
|
|
|
function add(uint a, uint b) public view returns (uint) {
|
|
uint c = a + b;
|
|
return c;
|
|
}
|
|
|
|
|
|
}
|
|
```
|
|
|
|
Ganache includes 10 accounts, and which each has 100 Eth in its account. These accounts can then be used to perform transactions on the blockchain. The server places itself on a certain port. In the example above, this port is TCP port 8545. This port will be used to connect from Remix to our blockchain and deploy our smart contract. Next, we compile the smart contract:
|
|
|
|

|
|
|
|
And if we get no errors, we can now deploy the contact to our blockchain. For this we now select the Deployment tab, and then for the Environment we select “Web3 Provider”. It should then pick up the first account address:
|
|
|
|

|
|
|
|
We should be all good to now deploy by clicking on the “Deploy” button, and Remix should give us a message that it has deployed the contract successfully.
|
|
|
|

|
|
|
|
Once we deploy our contact, we can use Remix to test it. In the following we see we can test the add() method for the contact, and add 5 and 3, with a result of 8:
|
|
|
|

|
|
|
|
Test the other functions, and check that they work.
|
|
|
|
## C Hashing
|
|
Open Zeppelin is open-source Solidity library that supports a wide range of functions that integrate into smart contracts in Ethereum. In the following we will implement a number of standard hashing methods, alongside a Base64 integration from Open Zeppelin:
|
|
|
|
```Solidity
|
|
pragma solidity ^0.8.0;
|
|
import "@openzeppelin/contracts/utils/Base64.sol";
|
|
import "@openzeppelin/contracts/utils/Strings.sol";
|
|
|
|
contract Hashit {
|
|
|
|
function getKeccak256(string memory str) public pure returns(bytes32){
|
|
return keccak256(abi.encodePacked(str));
|
|
}
|
|
|
|
function getSha256(string memory str) public pure returns (bytes32) {
|
|
return sha256(abi.encodePacked(str));
|
|
}
|
|
|
|
function getBase64(string memory str) public pure returns(string memory){
|
|
return Base64.encode(abi.encodePacked(str));
|
|
}
|
|
|
|
function getStringHex(uint256 str) public pure returns(string memory){
|
|
return Strings.toHexString(str);
|
|
}
|
|
|
|
function getString(uint256 str) public pure returns(string memory){
|
|
return Strings.toString(str);
|
|
}
|
|
}
|
|
```
|
|
|
|
With this, we get a number of solidity code integrations that enhance smart contracts:
|
|
|
|
The integration is fairly simple, and where we just pick the required solidity file integration (after reviewing it, of course). In the following we integrate with Base64 and Strings:
|
|
|
|
```
|
|
import "@openzeppelin/contracts/utils/Base64.sol";
|
|
import "@openzeppelin/contracts/utils/Strings.sol";
|
|
```
|
|
|
|
There are certain standard hash functions that integrate into Solidity. These include keccak256() and sha256():
|
|
|
|
```
|
|
function getKeccak256(string memory str) public pure returns(bytes32){
|
|
return keccak256(abi.encodePacked(str));
|
|
}
|
|
|
|
function getSha256(string memory str) public pure returns (bytes32) {
|
|
return sha256(abi.encodePacked(str));
|
|
}
|
|
```
|
|
|
|
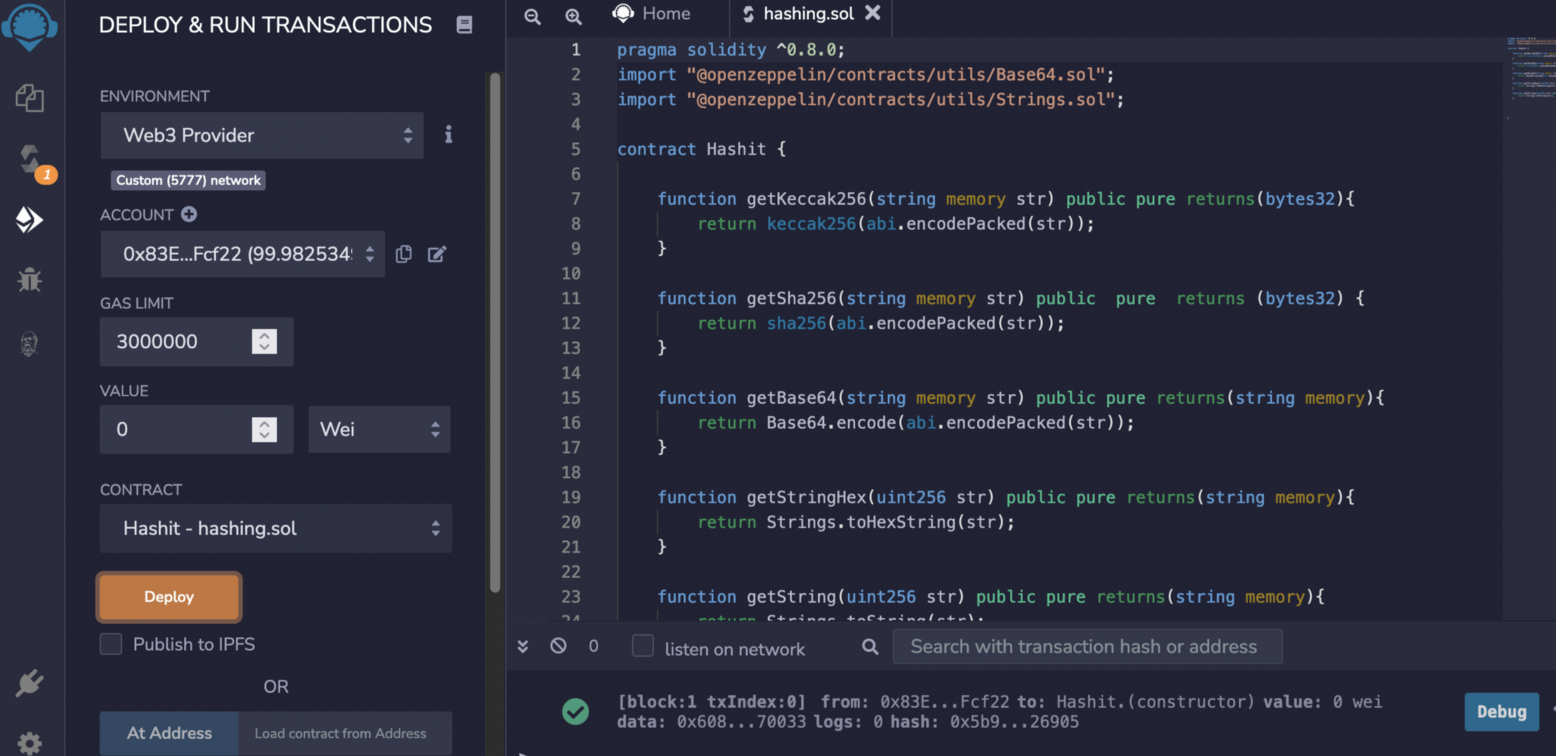
We can then create our smart contract in Remix [here], and compile the contract:
|
|
|
|

|
|
|
|
Now we can start our local blockchain with Ganache:
|
|
|
|
|
|
|
|
And then deploy our smart contact:
|
|
|
|
|
|
|
|
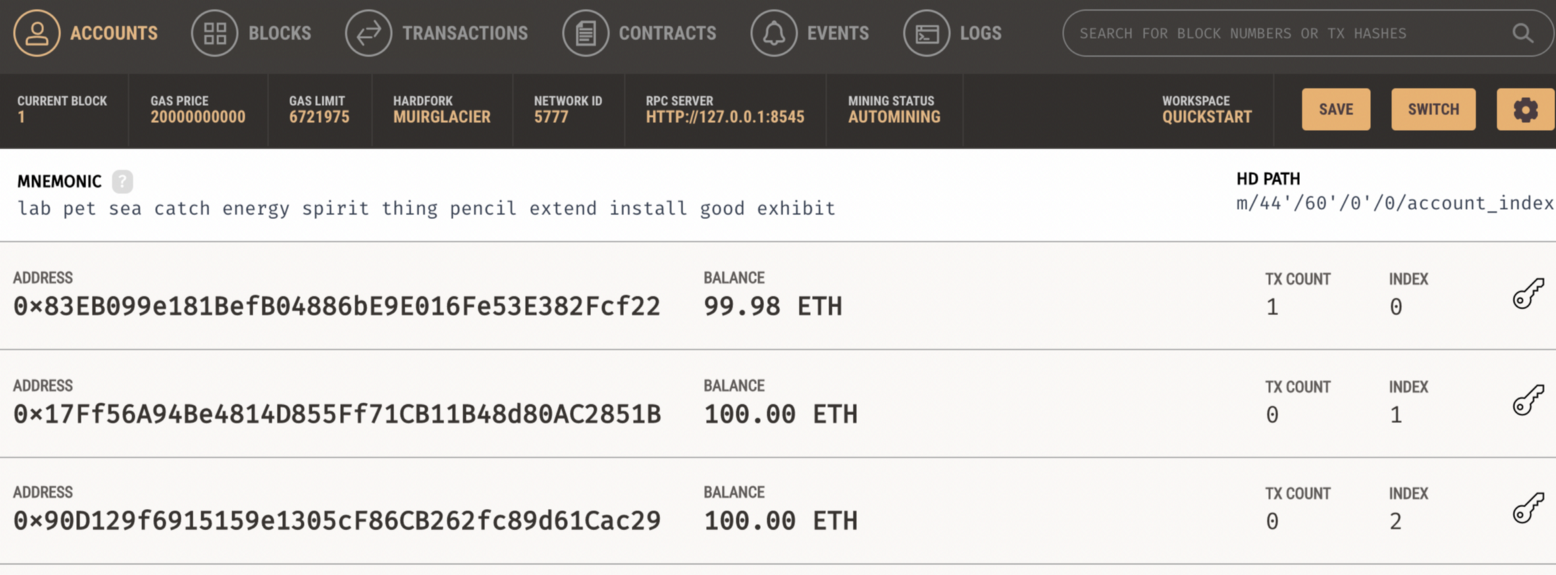
We then see that this has cost one of the accounts some amount of gas:
|
|
|
|
|
|
|
|
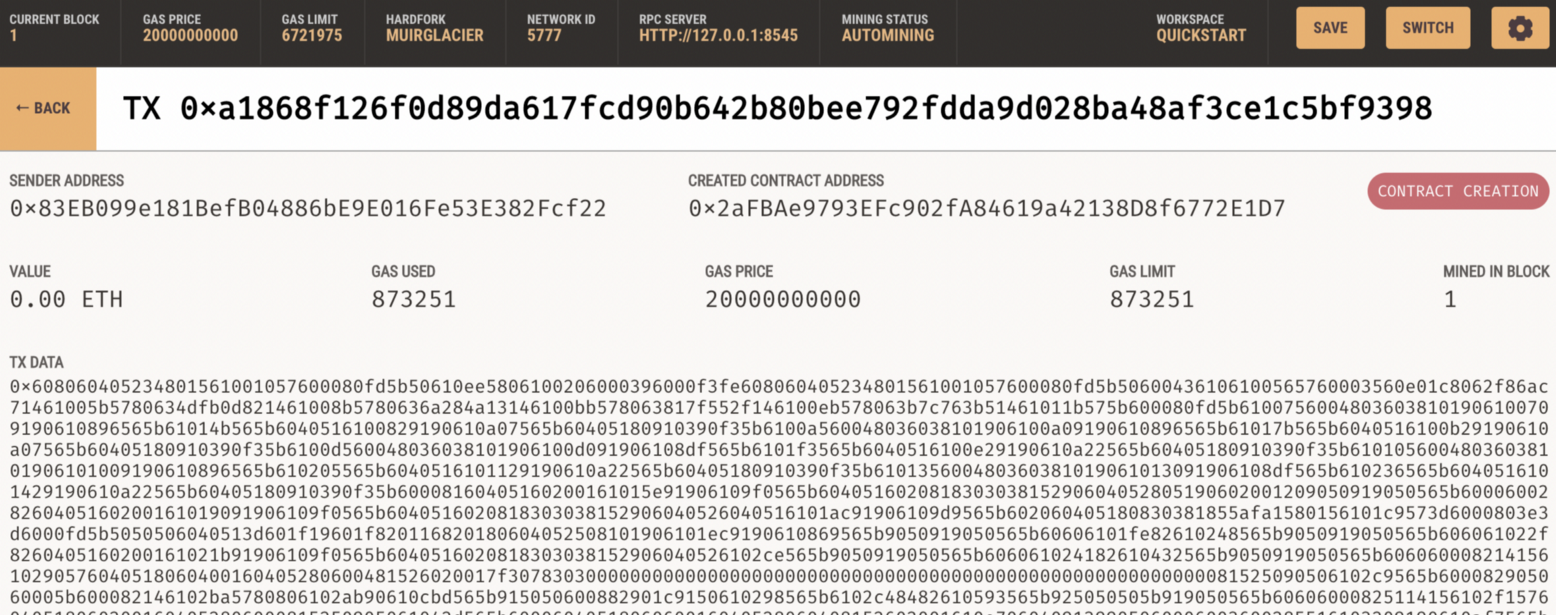
And then we see we have a contract:
|
|
|
|
|
|
|
|
Now we can go ahead and test the contract:
|
|
|
|
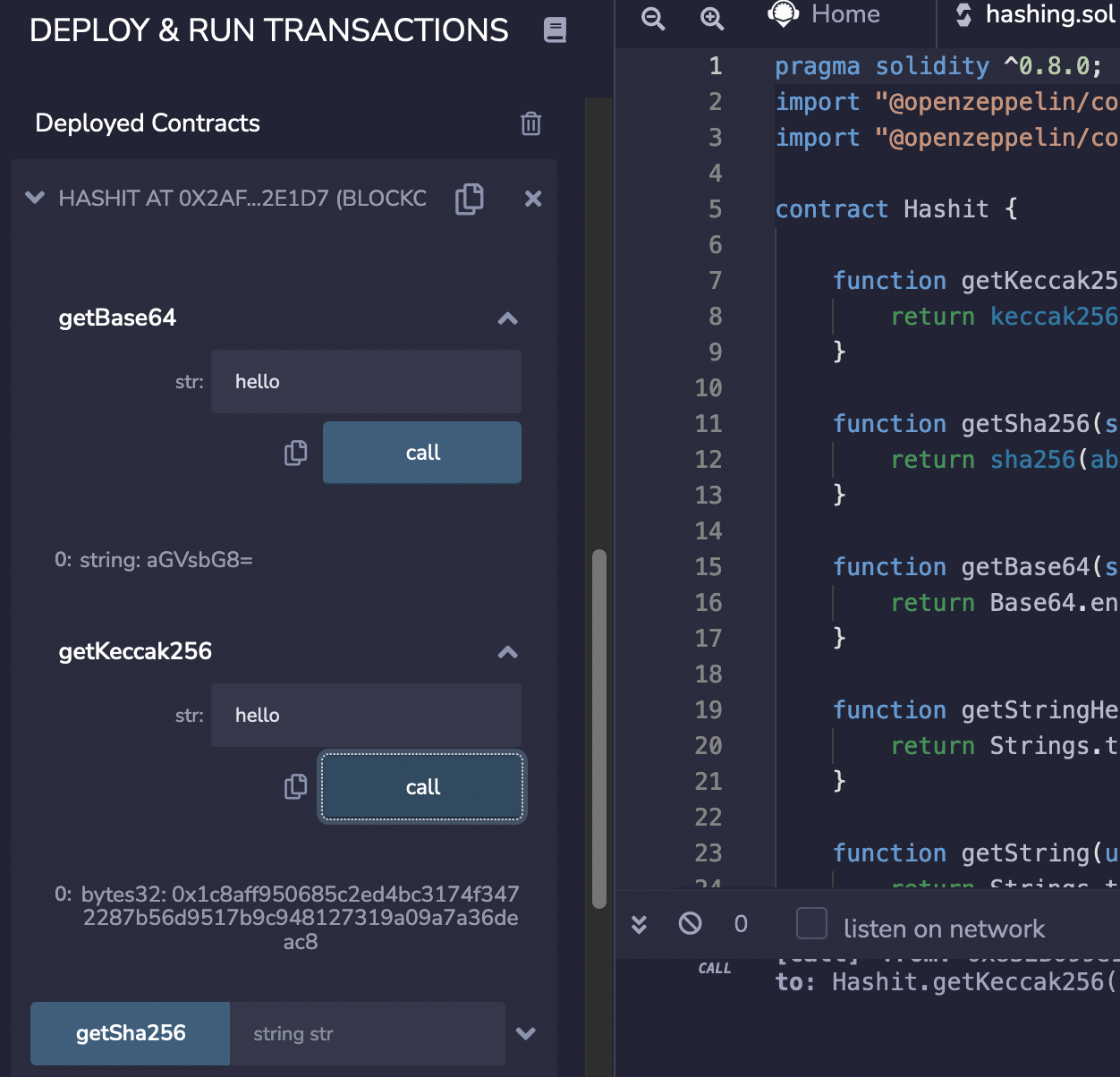
|
|
|
|
In this case we see that the Base64 string for “hello” is “aGVsbG8=”, and that the Keccak-256 hash for “hello” is “0x1c8aff950685c2ed4bc3174f3472287b56d9517b9c948127319a09a7a36deac8”. You can test this [here](https://asecuritysite.com/hash/s3?m=hello):
|
|
|
|
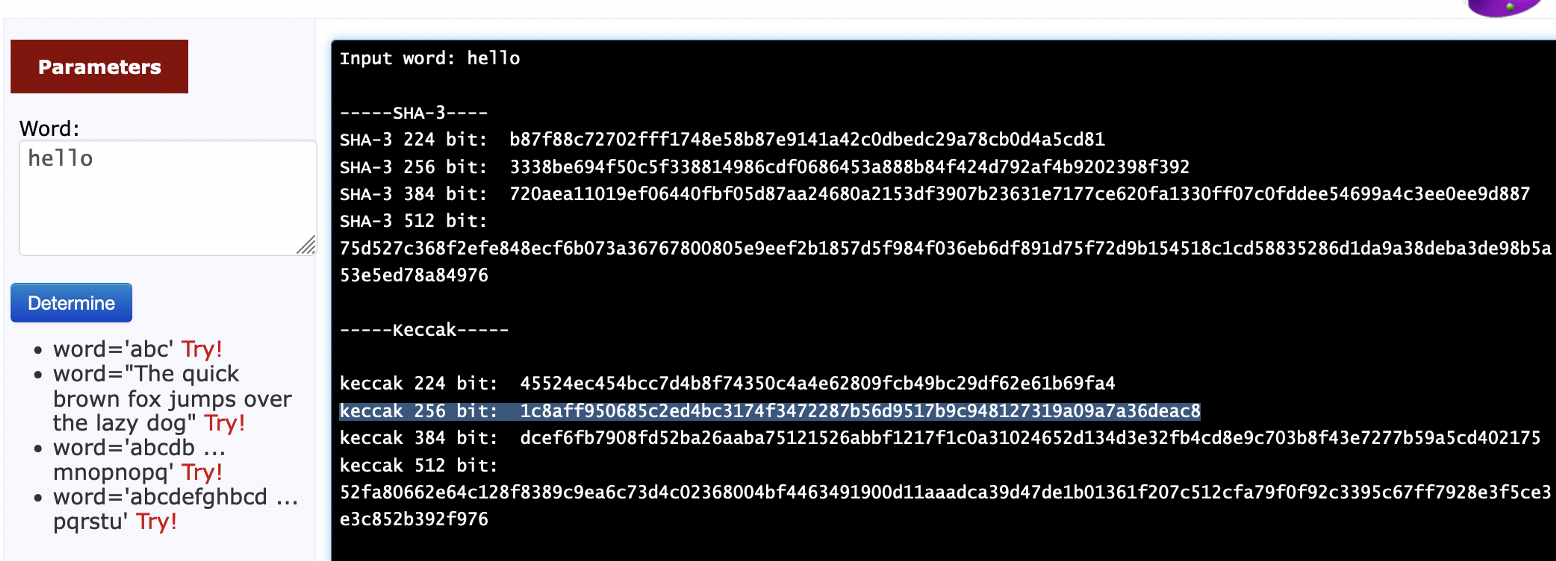
|
|
|
|
And [here](https://asecuritysite.com/Coding/ascii?ascii=hello) for Base64:
|
|
|
|
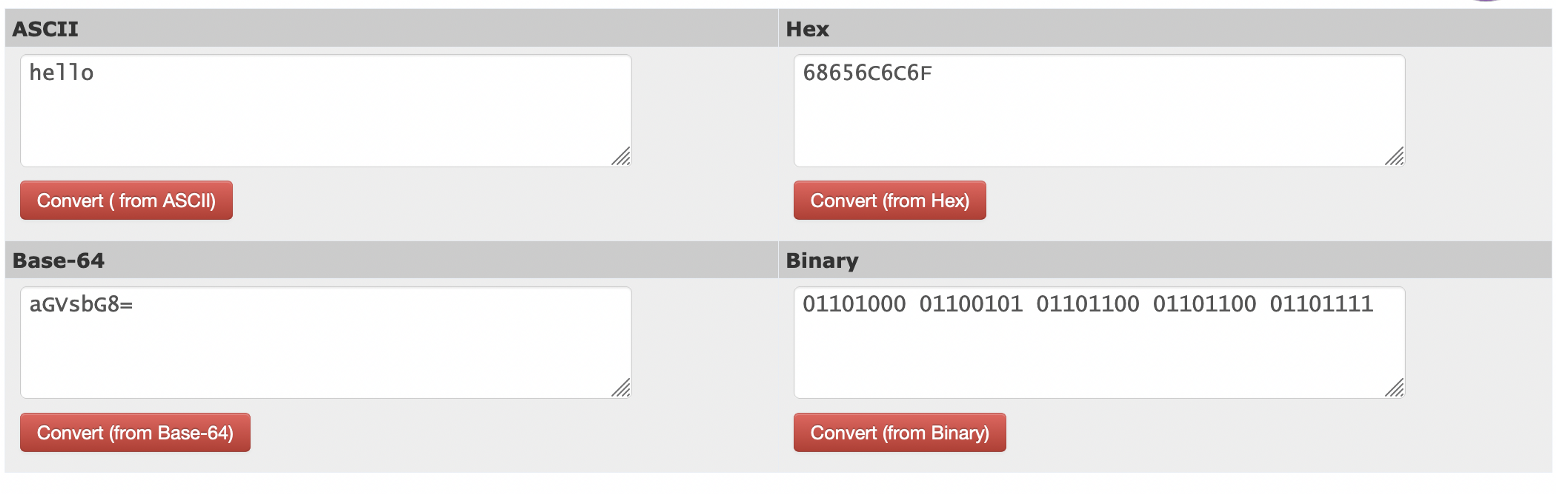
|
|
|
|
Now go ahead and test each of the functions, and prove that they work.
|
|
|
|
## D Post-quantum crypto
|
|
There are many examples of PQC [here](https://asecuritysite.com/pqc/).
|
|
|
|
What are the names of the finalists for the NIST standard for PQC related to digital signatures?
|
|
|
|
By analysing the results from this page [here](https://asecuritysite.com/pqc/pqc_sig). Which method do you think will win the competition?
|
|
|
|
What are the names of the finalists for the NIST standard for PQC related to key exchange mechanism?
|
|
|
|
By analysing the results from this page [here](https://asecuritysite.com/pqc/pqc_kem). Which method do you think will win the competition?
|
|
|
|
## E Light-weight crypto
|
|
There are many examples of light-weight cryptography [here](https://asecuritysite.com/light/).
|
|
|
|
What are the names of the finalists for the NIST standard for light-weight cryptography?
|
|
|
|
### E1
|
|
In many operations within public key methods we use the exponential operation:
|
|
|
|
g<sup>x</sup> (mod p)
|
|
|
|
If we compute the value of gx and then perform a (mod p) it is a very costly operation in terms of CPU as the value of gx will be large. A more efficient method it use Montgomery reduction and use pow(g,x,p).
|
|
|
|
```Python
|
|
import random
|
|
g=3
|
|
x= random.randint(2, 100)
|
|
n=997
|
|
res1 = g**x % n
|
|
res2= pow(g,x, n)
|
|
print (res1)
|
|
print (res2)
|
|
```
|
|
|
|
Repl.it: https://repl.it/@billbuchanan/powex
|
|
|
|
Now add some code to determine the time taken to perform each of the two operations, and compare them:
|
|
|
|
Can you now put each of the methods into a loop, and perform each calculation 1,000 times?
|
|
|
|
Now measure the times taken. What do you observe?
|
|
|
|
|
|
Now increase the range for x (so that it is relatively large) and make n a large prime number. What do you observe from the performance:
|
|
|
|
|
|
### E2
|
|
Normally light-weight crypto has to be fast and efficient. The XTEA method is one of the fastest around. Some standard open source code in Node.js is (use npm install xtea):
|
|
|
|
```Node.js
|
|
var xtea = require('xtea');
|
|
|
|
var plaintext = new Buffer('ABCDEFGH', 'utf8');
|
|
var key = new Buffer('0123456789ABCDEF0123456789ABCDEF', 'hex');
|
|
var ciphertext = xtea.encrypt( plaintext, key );
|
|
|
|
console.log('Cipher:\t'+ ciphertext.toString('hex') );
|
|
console.log('Decipher:\t'+ xtea.decrypt( ciphertext, key ).toString() );
|
|
```
|
|
|
|
Repl.it: https://repl.it/@billbuchanan/xteajs
|
|
|
|
Note: It you prefer to use Python, the code is [here](https://asecuritysite.com/light/xtea).
|
|
|
|
A sample run is:
|
|
|
|
```
|
|
Cipher: 52deb267335dd52a49837931c233cea8
|
|
Decipher: ABCDEFGH
|
|
```
|
|
|
|
|
|
|
|
What is the block and key size of XTEA?
|
|
|
|
|
|
|
|
Can you add some code to measure the time taken for 1,000 encryptions?
|
|
|
|
|
|
Can you estimate the number for encryption keys that could be tried per second on your system?
|
|
|
|
|
|
If possible, run the code on another machine, and estimate the rate of encryption keys that can be used per second:
|
|
|
|
|
|
|
|
### E3
|
|
RC4 is a stream cipher created by Ron Rivest and has a variable key length. Run the following Python code and test it:
|
|
|
|
```Python
|
|
import sys
|
|
def KSA(key):
|
|
keylength = len(key)
|
|
|
|
S = list(range(256))
|
|
|
|
j = 0
|
|
for i in range(256):
|
|
j = (j + S[i] + key[i % keylength]) % 256
|
|
S[i], S[j] = S[j], S[i] # swap
|
|
|
|
return S
|
|
|
|
|
|
def PRGA(S):
|
|
i = 0
|
|
j = 0
|
|
while True:
|
|
i = (i + 1) % 256
|
|
j = (j + S[i]) % 256
|
|
|
|
S[i], S[j] = S[j], S[i] # swap
|
|
|
|
K = S[(S[i] + S[j]) % 256]
|
|
yield K
|
|
|
|
def RC4(key):
|
|
S = KSA(key)
|
|
|
|
return PRGA(S)
|
|
|
|
|
|
key="0102030405"
|
|
|
|
plaintext = 'Hello'
|
|
|
|
if (len(sys.argv)>1):
|
|
plaintext=str(sys.argv[1])
|
|
|
|
if (len(sys.argv)>2):
|
|
key=str(sys.argv[2])
|
|
|
|
key = bytes.fromhex(key)
|
|
|
|
keystream = RC4(key)
|
|
print ("Keystream:\t", end='')
|
|
for i in range (0,15):
|
|
print (hex(next(keystream))[2:],end='')
|
|
|
|
print ("\nPlaintext:\t",plaintext)
|
|
print ("Cipher:\t\t",end='')
|
|
keystream = RC4(key)
|
|
|
|
for c in plaintext:
|
|
sys.stdout.write("%02X" % (ord(c) ^ next(keystream)))
|
|
|
|
print ("\n\nS-box: ",KSA(key))
|
|
```
|
|
Repl.it: https://repl.it/@billbuchanan/rc4tut
|
|
|
|
Now go to https://tools.ietf.org/html/rfc6229 and test a few key generation values and see if you get the same key stream.
|
|
|
|
Tests:
|
|
|
|
Key: 0102030405
|
|
|
|
Key stream (first six bytes):
|
|
|
|
Key:
|
|
|
|
Key stream (first six bytes):
|
|
|
|
Key:
|
|
|
|
Key stream (first six bytes):
|
|
|
|
Key:
|
|
|
|
Key stream (first six bytes):
|
|
|
|
How does the Python code produce a key stream length which matches the input data stream:
|
|
|
|
|
|
Can you test the code by decrypting the cipher stream (note: you just use the same code, and do the same operation again)?
|
|
|
|
|
|
RC4 uses an s-Box. Can you find a way to print out the S-box values for a key of “0102030405”?
|
|
|
|
|
|
What are the main advantages of having a variable key size and having a stream cipher in light-weight cryptography?
|
|
|
|
|
|
|
|
|
|
## F Zero-knowledge proof (ZKP)
|
|
|
|
### F.1
|
|
With ZKP, Alice can prove that he still knows something to Bob, without revealing her secret. At the basis of many methods is the Fiat-Shamir method:
|
|
|
|
|
|
Ref: https://asecuritysite.com/encryption/fiat
|
|
|
|
Repl.it: https://repl.it/@billbuchanan/zktut2
|
|
|
|
The following code implements some basic code for Fiat-Shamir, can you prove that for a number of values of x, that Alice will always be able to prove that she knows x.
|
|
|
|
x: Proved: Y/N
|
|
x: Proved: Y/N
|
|
x: Proved: Y/N
|
|
x: Proved: Y/N
|
|
|
|
The value of n is a prime number. Now increase the value of n, and determine the effect that this has on the time taken to compute the proof:
|
|
|
|
|
|
|
|
```Python
|
|
import sys
|
|
import random
|
|
|
|
n=97
|
|
|
|
g= 5
|
|
|
|
x = random.randint(1,5)
|
|
v = random.randint(n//2,n)
|
|
c = random.randint(1,5)
|
|
|
|
y= pow(g,x, n)
|
|
|
|
t = pow(g,v,n)
|
|
|
|
r = (v - c * x)
|
|
|
|
print r
|
|
if (r<0): r=-r
|
|
|
|
Result = ( pow(g,r,n)) * (pow(y,c,n)) % n
|
|
|
|
|
|
print 'x=',x
|
|
print 'c=',c
|
|
print 'v=',v
|
|
print 'P=',n
|
|
print 'G=',g
|
|
print '======'
|
|
print 't=',t
|
|
print 'r=',Result
|
|
if (t==Result):
|
|
print 'Alice has proven she knows x'
|
|
else:
|
|
print 'Alice has not proven she knows x'import sys
|
|
import random
|
|
import hashlib
|
|
import libnum
|
|
|
|
n=997
|
|
|
|
password="Hello"
|
|
|
|
g= 3
|
|
|
|
|
|
def pickg(p):
|
|
for x in range (1,p):
|
|
rand = x
|
|
exp=1
|
|
next = rand % p
|
|
|
|
while (next != 1 ):
|
|
next = (next*rand) % p
|
|
exp = exp+1
|
|
|
|
if (exp==p-1):
|
|
return rand
|
|
|
|
v = random.randint(1,n)
|
|
c = random.randint(1,n)
|
|
|
|
|
|
if (len(sys.argv)>1):
|
|
text=str(sys.argv[1])
|
|
|
|
if (len(sys.argv)>2):
|
|
v=int(sys.argv[2])
|
|
|
|
if (len(sys.argv)>3):
|
|
c=int(sys.argv[3])
|
|
|
|
if (len(sys.argv)>4):
|
|
n=int(sys.argv[4])
|
|
|
|
|
|
|
|
print("Password:\t",password)
|
|
x = int(hashlib.md5(password.encode()).hexdigest()[:8], 16) % n
|
|
|
|
g=pickg(n)
|
|
|
|
y= pow(g,x,n)
|
|
|
|
t = pow(g,v,n)
|
|
|
|
r = (v - c * x)
|
|
|
|
if (r<0):
|
|
Result = ( libnum.invmod(pow(g,-r,n),n) * pow(y,c,n)) % n
|
|
else:
|
|
Result = ( pow(g,r,n) * pow(y,c,n)) % n
|
|
|
|
print('\n======Agreed parameters============')
|
|
print('P=',n,'\t(Prime number)')
|
|
print('G=',g,'\t(Generator)')
|
|
|
|
|
|
print('\n======The secret==================')
|
|
print('x=',x,'\t(Alice\'s secret)')
|
|
|
|
print('\n======Random values===============')
|
|
print('c=',c,'\t(Bob\'s random value)')
|
|
print('v=',v,'\t(Alice\'s random value)')
|
|
|
|
print('\n======Shared value===============')
|
|
print('g^x mod P=\t',y)
|
|
print('r=\t\t',r)
|
|
|
|
print('\n=========Results===================')
|
|
print('t=g**v % n =\t\t',t)
|
|
print('( (g**r) * (y**c) )=\t',Result)
|
|
if (t==Result):
|
|
print('Alice has proven she knows password')
|
|
else:
|
|
print('Alice has not proven she knows x')
|
|
```
|
|
|
|
Repl.it: https://repl.it/@billbuchanan/zktut
|
|
|
|
### F.2
|
|
We can now expand this method by creating a password, and then making this the secret. Copy and run the code here:
|
|
|
|
https://asecuritysite.com/encryption/fiat2
|
|
|
|
Repl.it: https://repl.it/@billbuchanan/zktut2
|
|
|
|
Now test the code with different passwords?
|
|
|
|
|
|
How does the password get converting into a form which can be used in the Fiat-Shamir method?
|
|
|
|
|
|
|
|
### F.3
|
|
The Diffie-Hellman method can be used to perform a zero-knowledge proof implementation. Copy the code from the following link and verify that it works:
|
|
|
|
https://asecuritysite.com/encryption/diffiez
|
|
|
|
Repl.it: https://repl.it/@billbuchanan/diffiez
|
|
|
|
|
|
|
|
|
|
|